The first part of the TASC Math test consists of 40 multiple choice questions. Our free TASC Math practice test is a great option for your test prep and review. It includes a full set of challenging questions that cover all the major topics from the TASC blueprint. You may use a scientific calculator and you may consult the Mathematics Reference Sheet, which includes many important formulas.
Congratulations - you have completed .
You scored %%SCORE%% out of %%TOTAL%%.
Your performance has been rated as %%RATING%%
Your answers are highlighted below.
Question 1 |
Simplify:
(x6)(x5)
2x11 | |
2x30 | |
x11 | |
x30 |
Question 1 Explanation:
The correct answer is (C).When multiplying exponents with the same base, you should add the exponents:
(x6)(x5) = x(5 + 6)
= x11
(x6)(x5) = x(5 + 6)
= x11
Question 2 |
Solve for x:
3(x + 1) = 5(x − 2) + 7
−2 | |
2 | |
½ | |
3 |
Question 2 Explanation:
The correct answer is (D). Begin by distributing the 3 and the 5 through their respective parentheses, then combine like terms on each side of the equal sign:
3(x + 1) = 5(x − 2) + 7
3x + 3 = 5x − 10 + 7
3x + 3 = 5x − 3
Add 3 to both sides to maintain the equality:
3x + 6 = 5x
Subtract 3x from both sides and then divide the resulting equation by 2 to solve for x as follows:
6 = 2x
3 = x
3(x + 1) = 5(x − 2) + 7
3x + 3 = 5x − 10 + 7
3x + 3 = 5x − 3
Add 3 to both sides to maintain the equality:
3x + 6 = 5x
Subtract 3x from both sides and then divide the resulting equation by 2 to solve for x as follows:
6 = 2x
3 = x
Question 3 |
Calculate the volume of this can. The height of the can is 6 inches and the diameter of the lid is 3 inches (use 3.14 for pi).
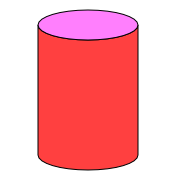
42.39 in3 | |
7.07 in3 | |
70.65 in3 | |
169.56 in3 |
Question 3 Explanation:
The correct answer is (A). The formula for the volume of a cylinder can be found on the formula reference sheet:
V = π r 2 h
We have the diameter of the lid, but we need the radius. The radius is equal to half the diameter (r = d/2), so r = 3/2 = 1.5 in. The given height is 6 in. Make the appropriate substitutions and solve for V, remember to follow the order of operations and evaluate the exponent before multiplying:
V = (3.14) * (1.5)2 * (6)
V = (3.14) * (2.25) * (6)
V = 42.39
V = π r 2 h
We have the diameter of the lid, but we need the radius. The radius is equal to half the diameter (r = d/2), so r = 3/2 = 1.5 in. The given height is 6 in. Make the appropriate substitutions and solve for V, remember to follow the order of operations and evaluate the exponent before multiplying:
V = (3.14) * (1.5)2 * (6)
V = (3.14) * (2.25) * (6)
V = 42.39
Question 4 |
10,000 meters = ?
1 kilometer | |
10 kilometers | |
100 kilometers | |
10,000 kilometers |
Question 4 Explanation:
The correct answer is (B). Notice that each answer choice is in kilometers. Recall that the prefix ‘kilo-’ indicates 1,000 and that 1 kilometer is equal to 1,000 meters. Dimensional analysis using the conversion factor 1 km = 1000 m can be used to calculate the answer:
$10{,}000 \text{ m} \ast \frac{1 \text{ km}}{1{,}000 \text{ m}} = 10 \text{ km}$
Notice that meters cancel and leave the answer in the desired units of kilometers.
$10{,}000 \text{ m} \ast \frac{1 \text{ km}}{1{,}000 \text{ m}} = 10 \text{ km}$
Notice that meters cancel and leave the answer in the desired units of kilometers.
Question 5 |
The probability that the Blue Comets score the first goal in any game is 90%. What is the probability of the Blue Comets scoring the first goal in 4 straight games?
0.81 | |
0.45 | |
0.729 | |
0.656 |
Question 5 Explanation:
The correct answer is (D). First recognize that the probability of the Blue Comets scoring the first goal in any single game is 90% regardless of whether they score first in any other game. This indicates that scoring first in consecutive games is a series of independent events. To find the probability of consecutive independent events occurring, calculate the product of their probabilities.
The probability of the team scoring first in 4 straight games is then:
0.9 * 0.9 * 0.9 * 0.9 = 0.6561, which rounds to 0.656.
The probability of the team scoring first in 4 straight games is then:
0.9 * 0.9 * 0.9 * 0.9 = 0.6561, which rounds to 0.656.
Question 6 |
Given ƒ(x) = 2x2 − 3x + 7, find ƒ(2.5)
5 | |
12 | |
19 | |
24.5 |
Question 6 Explanation:
The correct answer is (B). This is a function problem. A function relates an input to an output. To find ƒ(2.5), substitute 2.5 for every x in the original function and evaluate the expression:
ƒ(2.5) = 2(2.5)2 − 3(2.5) +7
ƒ(2.5) = 2(6.25) − 7.5 + 7
ƒ(2.5) = 12.5 − 7.5 + 7
ƒ(2.5) = 12
ƒ(2.5) = 2(2.5)2 − 3(2.5) +7
ƒ(2.5) = 2(6.25) − 7.5 + 7
ƒ(2.5) = 12.5 − 7.5 + 7
ƒ(2.5) = 12
Question 7 |
Diego’s current age is five times Martina’s age ten years ago. If Martina is currently m years old, what is Diego’s current age in terms of m?
5m | |
5m − 10 | |
5m − 50 | |
5m + (m − 10) |
Question 7 Explanation:
The correct answer is (C). Use the information and variables provided in the question to equate Diego’s age with Martina’s age. Begin by representing Martina’s age ten years ago in terms of m:
m − 10
So Diego’s current age is:
5(m − 10)
= 5m − 50
m − 10
So Diego’s current age is:
5(m − 10)
= 5m − 50
Question 8 |
How many different passcodes can be formed from the letters {A, B, C, D} if each letter can only be used once?
6 | |
24 | |
120 | |
720 |
Question 8 Explanation:
The correct answer is (B). Given that each letter can only be used once, and there are a total of 4 letters, the first character of the passcode can only be occupied by 4 different letters. After using the first letter, there are 3 letters remaining that can occupy the second spot; then 2 letters for the third spot, and only 1 letter for the last spot. The product of these values yields the total number of possibilities:
4 * 3 * 2 * 1 = 24
The solution can also be found using the formula for the total number of different arrangements of n distinct elements:
n! = n(n − 1)(n − 2)… * 1
4! = 4 * 3 * 2 * 1
4! = 24
4 * 3 * 2 * 1 = 24
The solution can also be found using the formula for the total number of different arrangements of n distinct elements:
n! = n(n − 1)(n − 2)… * 1
4! = 4 * 3 * 2 * 1
4! = 24
Question 9 |
The population density of an area can be computed by dividing the total population by the total land area. The population density of Rhode Island is 870.5 people/square mile and the population is 1,055,046. What is the area of Rhode Island?
8.25 mi2 | |
825 mi2 | |
1,212 mi2 | |
918 mi2 |
Question 9 Explanation:
The correct answer is (C).Use the definition provided in the first sentence of the question to set up an equation relating population density to area. Substitute the given values to then solve for the unknown area:
Population Density $= \frac{\text{Total Population}}{\text{Total Land Area}}$
870.5 People/sq.ml. $= \frac{1{,}055{,}046\text{ People}}{\text{Unknown Area}}$
Isolate the unknown total area by multiplying both sides by the unknown area and dividing both sides by the population density (870.5):
Unknown Area $= \frac{1{,}055{,}046\text{ People}}{870.5 \text{ People/sq.ml.}}$
Notice that the units of people cancel in the numerator and denominator, and that the computed area is in the expected units of square miles. This method of dimensional analysis is incredibly useful in validating a mathematical set up. The unknown area is then:
$\frac {1,055,046}{870.5} =$ 1,212 square miles.
Population Density $= \frac{\text{Total Population}}{\text{Total Land Area}}$
870.5 People/sq.ml. $= \frac{1{,}055{,}046\text{ People}}{\text{Unknown Area}}$
Isolate the unknown total area by multiplying both sides by the unknown area and dividing both sides by the population density (870.5):
Unknown Area $= \frac{1{,}055{,}046\text{ People}}{870.5 \text{ People/sq.ml.}}$
Notice that the units of people cancel in the numerator and denominator, and that the computed area is in the expected units of square miles. This method of dimensional analysis is incredibly useful in validating a mathematical set up. The unknown area is then:
$\frac {1,055,046}{870.5} =$ 1,212 square miles.
Question 10 |
What are the TWO solutions to the following equation?
x2 + 8x + 15 = 0
−5 | |
−3 | |
−2 | |
2 | |
3 | |
5 |
Question 10 Explanation:
The correct answers are (A) and (B). One easy way to solve a problem like this is by plugging each answer choice into the equation to see which values yield a true statement. Alternatively, the values can be calculated by factoring the expression:
In order to factor the quadratic, we need to find two factors of 15 (the constant term) that sum up to 8 (the coefficient of x):
15 = 3 * 5
8 = 3 + 5
So 3 and 5 are the two factors that meet our requirement.
The fully factored form of the quadratic is:
(x + 3)(x + 5) = 0
Recall that if ab= 0, then either a = 0, or b = 0.
In this case, (x + 3)(x + 5) = 0
So either x + 3 = 0, or x + 5 = 0
That is, either x = −3, or x = −5
The roots of the quadratic are −3, and −5
In order to factor the quadratic, we need to find two factors of 15 (the constant term) that sum up to 8 (the coefficient of x):
15 = 3 * 5
8 = 3 + 5
So 3 and 5 are the two factors that meet our requirement.
The fully factored form of the quadratic is:
(x + 3)(x + 5) = 0
Recall that if ab= 0, then either a = 0, or b = 0.
In this case, (x + 3)(x + 5) = 0
So either x + 3 = 0, or x + 5 = 0
That is, either x = −3, or x = −5
The roots of the quadratic are −3, and −5
Question 11 |
$\sqrt[3]{-8} = \; ?$
Undefined | |
−2 | |
2 | |
4 |
Question 11 Explanation:
The correct answer is (B). This problem asks for the cube root of −8. The cube root of a number is the value that, when cubed (multiplied with itself 3 times), gives the number inside of the radical. Remember that a negative number raised to an even exponent gives a positive result, but when raised to an odd exponent gives a negative result. Consequently, the cube root of −8 will be a negative number. It should also be apparent that squaring 3 gives a value greater than 8, so cubing 3 would give a value much larger than 8. Trying −2 as the likely possibility:
−2 * −2 = 4 * −2 = −8. So, −2 is the cube root of −8.
−2 * −2 = 4 * −2 = −8. So, −2 is the cube root of −8.
Question 12 |
Each player on the high school football team has been weighed, and the data are shown in the box-and-whisker plot below.
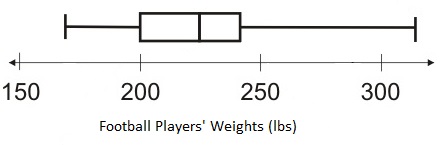
Based on this box-and-whisker plot, which of the following TWO statements are accurate?
The heaviest player weighs 300 lbs. | |
One-fourth of the players weigh less than 200 lbs. | |
The median player weighs 245 lbs. | |
The lightest player weighs 200 lbs. | |
The median player weighs 225 lbs. | |
At least 2 players weigh more than 300 lbs. |
Question 12 Explanation:
The correct answers are (B) and (E). Here is the meaning of each part of the box-and-whisker plot:
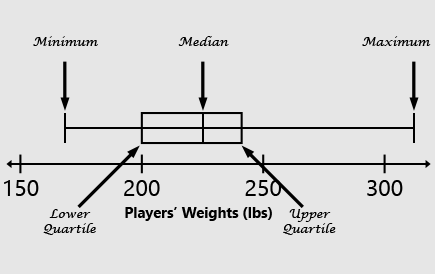
In this example, the minimum value represents the lightest player on the team and the maximum value represents the heaviest player on the team. The median value is the player who is at the midpoint of the distribution. The quartile values divide the distribution into fourths.
Since the lower quartile is at 200, it is accurate to say that one-fourth of the players weigh less than 200 lbs. It is also clear from the plot that the median weight is approximately 225 lbs.

In this example, the minimum value represents the lightest player on the team and the maximum value represents the heaviest player on the team. The median value is the player who is at the midpoint of the distribution. The quartile values divide the distribution into fourths.
Since the lower quartile is at 200, it is accurate to say that one-fourth of the players weigh less than 200 lbs. It is also clear from the plot that the median weight is approximately 225 lbs.
Question 13 |
$3^{-2} = \;?$
$−9$ | |
$−6$ | |
$9$ | |
$\dfrac{1}{9}$ |
Question 13 Explanation:
The correct answer is (D). To evaluate a base raised to a negative exponent that is in the numerator, rewrite the expression with the base and exponent in the denominator, and rewrite the negative exponent as a positive exponent. In cases where the base raised to a negative exponent is in the denominator, rewrite the base and exponent in the numerator, and switch the sign of the exponent:
$a^{−n} = \dfrac{1}{a^n}$
$3^{−2} = \dfrac{1}{3^2} = \dfrac{1}{9}$
$a^{−n} = \dfrac{1}{a^n}$
$3^{−2} = \dfrac{1}{3^2} = \dfrac{1}{9}$
Question 14 |
Calculate the value of x for the right triangle shown below.
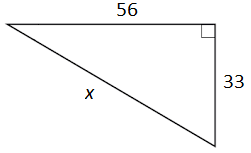
66 | |
89 | |
56 | |
65 |
Question 14 Explanation:
The correct answer is (D). The Pythagorean theorem can be used to find a missing segment of a right triangle if two side lengths are given. The theorem relates the legs of a right triangle to its hypotenuse as a2+ b2 = c2, where a and b are the legs and c is the hypotenuse. The hypotenuse is the longest side in a right triangle and is always opposite the right angle.
Substitute the known values into their appropriate places and solve for the unknown side length:
332 + 562 = c2
Evaluate the squares:
1,089 + 3,136 = c2
4,225 = c2
Evaluate the square root of both sides:
$\sqrt{c^2} = \sqrt{4{,}225}$
$c = 65$
Substitute the known values into their appropriate places and solve for the unknown side length:
332 + 562 = c2
Evaluate the squares:
1,089 + 3,136 = c2
4,225 = c2
Evaluate the square root of both sides:
$\sqrt{c^2} = \sqrt{4{,}225}$
$c = 65$
Question 15 |
What is the probability of selecting a male from a group of 4 males and 8 females?
$\dfrac{1}{3}$ | |
$\dfrac{1}{2}$ | |
$\dfrac{2}{3}$ | |
$\dfrac{4}{5}$ |
Question 15 Explanation:
The correct answer is (A). To find the probability of selecting a male, you need to divide the total number of males by the total number of people:
$P(\text{M}) = \frac{\text{Number of Males}}{\text{Total Number of People}}$
$P(\text{M}) = \dfrac{4}{12}$
$P(\text{M}) = \dfrac{1}{3}$
$P(\text{M}) = \frac{\text{Number of Males}}{\text{Total Number of People}}$
$P(\text{M}) = \dfrac{4}{12}$
$P(\text{M}) = \dfrac{1}{3}$
Question 16 |
Devon owns a house cleaning company and has to give price quotes to potential customers. He figures out his price by assuming a \$25 base charge and then adding \$8 for each bathroom and \$4 for each other room.
If he uses P to represent the price, B for bathroom, and R for other rooms, which of the following represents his price quote formula?P = 25 + 12(BR) | |
P = 25 + 8B + 4R | |
P = 25(4R + 8B) | |
P = (4)(8)(R + B) + 25 |
Question 16 Explanation:
The correct answer is (B). The price quote, P, will be equal to the total amount of charges. It’s given that there is a \$25 base charge, so we can begin by writing the price quote as P = \$25.
To this base charge of \$25, \$8 per each bathroom, represented by the variable B, is added; our price quote is now P = \$25 + \$8B.
Lastly, \$4 per each other room, R, is added, and the final price quote is P = \$25 + \$8B + \$4R, or P = 25 + 8B + 4R.
To this base charge of \$25, \$8 per each bathroom, represented by the variable B, is added; our price quote is now P = \$25 + \$8B.
Lastly, \$4 per each other room, R, is added, and the final price quote is P = \$25 + \$8B + \$4R, or P = 25 + 8B + 4R.
Question 17 |
Solve for x:
log2(x) = 4
2 | |
4 | |
8 | |
16 |
Question 17 Explanation:
The correct answer is (D). This is a logarithm problem. A logarithm is the inverse operation to exponentiation. It is helpful to remember that log2(x), is read “log base 2 of x” as then all you need to recall is that the base raised to the value on the right hand side of the equation is equal to x. Stated otherwise:
y = bx is equivalent to logb(y) = x
Using this relationship:
log2(x) = 4 is equivalent to 24 = x
x = 16
y = bx is equivalent to logb(y) = x
Using this relationship:
log2(x) = 4 is equivalent to 24 = x
x = 16
Question 18 |
Simplify:
(7y2 + 3xy − 9) − (2y2 + 3xy − 5)
5y2 − 4 | |
9y2 + 6xy − 14 | |
5y2 + 4 | |
5y2 + 6xy − 14 |
Question 18 Explanation:
The correct answer is (A). When subtracting polynomials the first step is to distribute the negative sign through the parentheses. This changes the sign on each term inside the parentheses:
7y2 + 3xy − 9 − 2y2 − 3xy + 5
Arrange like terms next to each other (optional):
7y2 − 2y2+ 3xy − 3xy − 9 + 5
Combine like terms to compute the answer:
5y2 − 4
7y2 + 3xy − 9 − 2y2 − 3xy + 5
Arrange like terms next to each other (optional):
7y2 − 2y2+ 3xy − 3xy − 9 + 5
Combine like terms to compute the answer:
5y2 − 4
Question 19 |
What is the solution set for x2 + 25 = 0?
−5i | |
−5 | |
5i | |
± 5i |
Question 19 Explanation:
The correct answer is (D). The solution set is the collection of values that when substituted for x, yield a true statement. Begin by isolating and solving for the variable:
$x^2 + 25 = 0$
$x^2 = -25$
$x = \pm \sqrt{-25}$
While the square root of a negative REAL number is undefined, the square root of an imaginary number can be evaluated using the definition:
$\sqrt{-1} = i$
Rewriting the equation for $x$:
$x = \pm \sqrt{(25)(-1)}$
$x = \pm \sqrt{25} \sqrt{-1}$
$x = \pm 5i$
$x^2 + 25 = 0$
$x^2 = -25$
$x = \pm \sqrt{-25}$
While the square root of a negative REAL number is undefined, the square root of an imaginary number can be evaluated using the definition:
$\sqrt{-1} = i$
Rewriting the equation for $x$:
$x = \pm \sqrt{(25)(-1)}$
$x = \pm \sqrt{25} \sqrt{-1}$
$x = \pm 5i$
Question 20 |
In a coordinate plane, triangle ABC has coordinates: (−2,7), (−3,6), and (4,5). If triangle ABC is reflected over the y-axis, what are the coordinates of the new image?
(−2,−7), (−3,−6), (−4,−5) | |
(−2,−7), (−3,−6), (4,−5) | |
(2,7), (3,6), (−4,5) | |
(2,7), (3,6), (4,5) |
Question 20 Explanation:
The correct answer is (C). One way to solve this problem is to draw the figure and then count how many units each point is from the y-axis, and count that many units in the opposite direction. A more efficient method is to recognize that reflecting over the y-axis causes the x-value to switch sign and does not influence the y-value of the point.
Reflecting (−2,7), (−3,6), (4,5) across the y-axis produces the points (2,7), (3,6), (−4,5).
Reflecting (−2,7), (−3,6), (4,5) across the y-axis produces the points (2,7), (3,6), (−4,5).
Question 21 |
Consider the list:
2, 2, 3, 5, 9, 11, 17, 21
If the number 23 is added to the list, which measurement will NOT change?
mean | |
median | |
mode | |
range |
Question 21 Explanation:
The correct answer is (C). The mode will not change. The mode is the number that appears the most frequently; in this case it is 2. The remaining measures will change:
The mean is the average, and in this case it will increase because a number larger than the current average is added to the list.
The median is the number in the middle, and it will change from 7 to 9.
The range is the difference between the highest and lowest numbers and will change from 19 to 21 because a new maximum value is added to the list (21 − 2 = 19 and 23 − 2 = 21).
The mean is the average, and in this case it will increase because a number larger than the current average is added to the list.
The median is the number in the middle, and it will change from 7 to 9.
The range is the difference between the highest and lowest numbers and will change from 19 to 21 because a new maximum value is added to the list (21 − 2 = 19 and 23 − 2 = 21).
Question 22 |
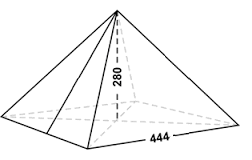
Calculate the volume of the pyramid. The height is 280 feet and the length of each base is 444 feet.
18,399,360 ft3 | |
55,198,080 ft3 | |
41,440 ft3 | |
123,200 ft3 |
Question 22 Explanation:
The correct answer is (A). Use the formula for the volume of a pyramid that is provided on the Mathematics Reference Sheet:
$V = \frac{1}{3}Bh$
Note: The letter B represents the area of the base, which is length × width. Evaluate B, then substitute its value and the given height, h, into the volume equation:
B = 444 × 444 = 197,136
V = (1/3)(197,136)(280)
V = 18,399,360
$V = \frac{1}{3}Bh$
Note: The letter B represents the area of the base, which is length × width. Evaluate B, then substitute its value and the given height, h, into the volume equation:
B = 444 × 444 = 197,136
V = (1/3)(197,136)(280)
V = 18,399,360
Question 23 |
Which of the following is equivalent to (7x + 3y)(8x + 5y)?
7x2 + 23xy + 5y2 | |
7x2 + 24xy + 8y2 | |
56x2 + 59xy + 15y2 | |
56x2 + 35xy + 15y2 |
Question 23 Explanation:
The correct answer is (C). Use the distributive property to multiply each term in the first parentheses through the second parentheses. When dealing with binomial expressions (those of the form (x ± y)(x ± y)), this method is commonly referred to as the FOIL Method:
Multiply the First two terms, then the Outer two terms, then the Inner two terms, and then the Last two terms. Then combine like terms to calculate the answer:
(7x + 3y)(8x + 5y)
56x2 + 35xy + 24xy + 15y2
56x2 + 59xy + 15y2
Multiply the First two terms, then the Outer two terms, then the Inner two terms, and then the Last two terms. Then combine like terms to calculate the answer:
(7x + 3y)(8x + 5y)
56x2 + 35xy + 24xy + 15y2
56x2 + 59xy + 15y2
Question 24 |
$\dfrac{7}{8} \div \dfrac{9}{5} = \; ?$
$\dfrac{7}{40}$ | |
$\dfrac{63}{40}$ | |
$\dfrac{40}{72}$ | |
$\dfrac{35}{72}$ |
Question 24 Explanation:
The correct answer is (D). Division by a fraction is equivalent to multiplying by the fraction’s reciprocal. The reciprocal is the fraction resulting from switching the numerator with the denominator. Rewrite the original problem as multiplication by the reciprocal to solve:
$\dfrac{7}{8} ÷ \dfrac{9}{5} = \dfrac{7}{8} \ast \dfrac{5}{9}$
$ = \dfrac{7 \ast 5}{8 \ast 9} = \dfrac{35}{72}$
$\dfrac{7}{8} ÷ \dfrac{9}{5} = \dfrac{7}{8} \ast \dfrac{5}{9}$
$ = \dfrac{7 \ast 5}{8 \ast 9} = \dfrac{35}{72}$
Question 25 |
Which scatter plot shows weak negative correlation?

#1 | |
#2 | |
#3 | |
#4 |
Question 25 Explanation:
The correct answer is (B). With positive correlations, as one variable increases, the other variable increases as well. This results in a scatter plot showing a positive slope. With negative correlations, as one variable increases, the other variable decreases (increasing x values result in decreasing y values). Graphs #2 and #4 show negative correlation because the y value decreases as the x value increases.
The closer the data points come to making a straight line, the higher the correlation between the two variables, or the stronger the relationship. The further the data points are from showing a straight line, the weaker the correlation. Since the data points in Graph #2 are not grouped tightly along a line, it indicates a weak correlation.
#1 Shows no correlation.
#2 Shows weak negative correlation.
#3 Shows strong positive correlation.
#4 Shows strong negative correlation.
The closer the data points come to making a straight line, the higher the correlation between the two variables, or the stronger the relationship. The further the data points are from showing a straight line, the weaker the correlation. Since the data points in Graph #2 are not grouped tightly along a line, it indicates a weak correlation.
#1 Shows no correlation.
#2 Shows weak negative correlation.
#3 Shows strong positive correlation.
#4 Shows strong negative correlation.
Question 26 |
There are 10 red marbles, 4 blue marbles, and 7 white marbles in a jar. One marble is chosen at random and then returned to the jar, and then a second marble is chosen at random. What is the probability that both of the marbles chosen are white?
$\dfrac{1}{3}$ | |
$\dfrac{1}{9}$ | |
$\dfrac{1}{6}$ | |
$\dfrac{2}{3}$ |
Question 26 Explanation:
The correct answer is (B). To calculate the probability that an event occurs, divide the number of possible successful events by the total number of events. In this case, a success is selecting a white marble, and the total number of events is the total number of marbles. Because the first selected marble is returned to the jar, the second selection does not depend on the first selection. To find the probability of consecutive independent events occurring, calculate the product of their probabilities.
The probability of selecting a white marble is:
$\dfrac{7 \text{ White Marbles}}{10 + 4 + 7 \text{ Total Marbles}}$
$= \dfrac{7}{21} = \dfrac{1}{3}$
To find the probability of selecting 2 white marbles in row:
$\dfrac{1}{3} \ast \dfrac{1}{3} = \dfrac{1}{9}$
The probability of selecting a white marble is:
$\dfrac{7 \text{ White Marbles}}{10 + 4 + 7 \text{ Total Marbles}}$
$= \dfrac{7}{21} = \dfrac{1}{3}$
To find the probability of selecting 2 white marbles in row:
$\dfrac{1}{3} \ast \dfrac{1}{3} = \dfrac{1}{9}$
Question 27 |
Investors use P/E Ratios to measure the relative value of stock shares. The P/E Ratio is calculated by dividing the price per share by the earnings per share. The earnings per share is calculated by dividing the company's net income by its total number of shares:
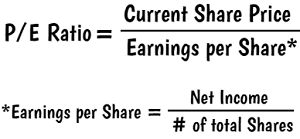
The Cool Cola Company has a P/E Ratio of 9.5. They have 56,650 shares of stock outstanding and their net income is $83,842. What is their current share price?
14.06 | |
0.156 | |
6.42 | |
1.4 |
Question 27 Explanation:
The correct answer is (A). Begin by using the given net income and number of total shares to calculate the earnings per share. Then, substitute the given P/E Ratio and earnings per share into the first equation to solve for the current share price:
Earnings per Share $= \dfrac{\$83{,}842}{56{,}650} = 1.48$
Substituting this and the P/E Ratio into the first equation:
$9.5 = \dfrac{\text{Net Income}}{1.48}$
Net Income $= 9.5 \ast 1.48 = 14.06$
Earnings per Share $= \dfrac{\$83{,}842}{56{,}650} = 1.48$
Substituting this and the P/E Ratio into the first equation:
$9.5 = \dfrac{\text{Net Income}}{1.48}$
Net Income $= 9.5 \ast 1.48 = 14.06$
Question 28 |
Write 54 = 625 in logarithmic form.
log4(5) = 625 | |
log4(625) = 5 | |
log5(625) = 4 | |
log5(4) = 625 |
Question 28 Explanation:
The correct answer is (C). It is very helpful to familiarize oneself with the relationship between logarithms and exponents and to be able to convert from one form to the other. The relationship is defined as follows:
y = bx is equivalent to logb(y) = x
Using the relationship given, 54 = 625 can be rewritten as log5(625) = 4.
y = bx is equivalent to logb(y) = x
Using the relationship given, 54 = 625 can be rewritten as log5(625) = 4.
Question 29 |
$8^{\frac{2}{3}} = \; ?$
256 | |
64 | |
48 | |
4 |
Question 29 Explanation:
The correct answer is (D). Every exponent can be written as a fraction. The numerator of a fractional exponent indicates raising the base to the power of the numerator. The denominator of a fractional exponent indicates evaluating the nth root of the base, where n is the denominator.
Applying the cube root first is recommended to produce a smaller number that can easily be raised to the power of 2:
$8^{\frac{2}{3}} = \left(8^{\frac{1}{3}}\right)^2 = (2)^2 = 4$
Alternatively, 8 can be first squared to give 64 which when cube rooted gives 4. Both routes give the same answer. It is also beneficial to familiarize yourself with the different forms that exponents and radicals can be written.
In this case $8^{\frac{2}{3}}$ could also be written as $\sqrt[3]{8^2}$
Applying the cube root first is recommended to produce a smaller number that can easily be raised to the power of 2:
$8^{\frac{2}{3}} = \left(8^{\frac{1}{3}}\right)^2 = (2)^2 = 4$
Alternatively, 8 can be first squared to give 64 which when cube rooted gives 4. Both routes give the same answer. It is also beneficial to familiarize yourself with the different forms that exponents and radicals can be written.
In this case $8^{\frac{2}{3}}$ could also be written as $\sqrt[3]{8^2}$
Question 30 |
Two points are plotted on a number line: −11.2 and 3.3. What is the distance between these two points?
7.9 | |
−7.9 | |
14.5 | |
−14.5 |
Question 30 Explanation:
The correct answer is (C). The distance between points A and B on a number line is the absolute value of the difference between those two points. Distance is always a positive value. Evaluate the difference between the points and then apply the absolute value:
AB = |b − a| or |a − b|
= |−11.2 − 3.3|
= |−14.5|
= 14.5
Recall that the absolute value of a number is its distance from 0, it is always positive.
AB = |b − a| or |a − b|
= |−11.2 − 3.3|
= |−14.5|
= 14.5
Recall that the absolute value of a number is its distance from 0, it is always positive.
Question 31 |
Which TWO of the following expressions are undefined in the set of real numbers?
$\sqrt{16}$ | |
$\sqrt{−9}$ | |
$\sqrt{0}$ | |
$\dfrac{5.4}{0}$ | |
$\sqrt[3]{−8}$ | |
$\sqrt{5.29}$ |
Question 31 Explanation:
The correct answers are (B) and (D). The square root of a number is the value that when multiplied with itself gives the number inside the square root, for example: $\sqrt{16}$ = ±4, because 4 * 4 = 16, and −4 * −4 = 16.
Notice that answer choice (B) shows a negative value inside the square root. This answer, $\sqrt{−9}$, must be undefined, because there is no real number that when multiplied with itself will give −9. All real numbers, when squared, give a positive value.
Answer choice (D) shows division by 0, which is always undefined.
Notice that answer choice (B) shows a negative value inside the square root. This answer, $\sqrt{−9}$, must be undefined, because there is no real number that when multiplied with itself will give −9. All real numbers, when squared, give a positive value.
Answer choice (D) shows division by 0, which is always undefined.
Question 32 |
Kiara has a budget of \$300 for her holiday spending and decides to buy shoes for her grandchildren. If each pair of shoes costs \$40, and Kiara has n grandchildren, which of the following inequalities represents her budget constraint?
40n > 300 | |
40 + n > 300 | |
40 + n ≤ 300 | |
40n ≤ 300 |
Question 32 Explanation:
The correct answer is (D). If Kiara buys n pairs of shoes at a cost of \$40 each, she pays \$40n. Since she only has \$300 to spend, \$40n must be less than or equal to $300:
40n ≤ 300
40n ≤ 300
Question 33 |
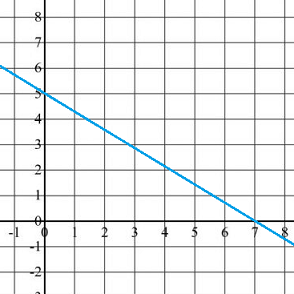
What is the slope of the line that passes through points (0,5) and (7,0) on the coordinate plane shown below?
$−\dfrac{7}{5}$ | |
$−\dfrac{5}{7}$ | |
$\dfrac{5}{7}$ | |
$\dfrac{7}{5}$ |
Question 33 Explanation:
The correct answer is (B). The slope of a line, which can be remembered as “the rise over the run,” is the change in y values divided by the change in x values across two points on a line. Written algebraically, the slope is defined as:
$m = \dfrac{y_2 − y_1}{x_2 − x_1}$
Substitute the given points (0,5) and (7,0) into the equation to calculate the slope:
$m = \dfrac{0 − 5}{7 − 0} = −\dfrac{5}{7}$
$m = \dfrac{y_2 − y_1}{x_2 − x_1}$
Substitute the given points (0,5) and (7,0) into the equation to calculate the slope:
$m = \dfrac{0 − 5}{7 − 0} = −\dfrac{5}{7}$
Question 34 |
Which of the following equations represents y in terms of x for all ordered pairs listed?
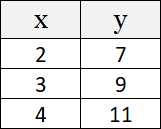
y = 4x ÷ 3 | |
y = 2x + 3 | |
y = x + 5 | |
y = 3x2 |
Question 34 Explanation:
The correct answer is (B). By inspecting the ordered pairs, it can be seen that as the x value increases by 1, the y value increases by 2. This indicates a linear relationship, and the answer choice containing x2 can be eliminated. Using the definition of the slope, which is calculated as:
$m = \dfrac{9 − 7}{3 − 2} = 2$
The answer must be y = 2x + 3. This answer can be further verified by substituting each ordered pair into the equation, for example:
11 = 2(4) + 3
11 = 8 + 3
11 = 11
$m = \dfrac{9 − 7}{3 − 2} = 2$
The answer must be y = 2x + 3. This answer can be further verified by substituting each ordered pair into the equation, for example:
11 = 2(4) + 3
11 = 8 + 3
11 = 11
Question 35 |
The graph provided shows the change in velocity of a rocket from time 0 to time 10. During what span of time is the rocket’s velocity decreasing?
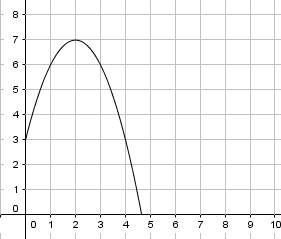
0 to 2 | |
0 to 4.6 | |
2 to 4.6 | |
3 to 4.6 |
Question 35 Explanation:
The correct answer is (C). The horizontal axis represents time and the vertical axis represents velocity. The rocket starts at a positive velocity, 3, and continues increasing in velocity until hour 2. At hour 2 the rocket reaches its apex and after hour 2 its velocity decreases until reaching a minimum at hour 4.6. The rocket’s velocity decreases over the hours 2 to 4.6.
Question 36 |
31 + 20 − 13 = ?
0 | |
2 | |
3 | |
4 |
Question 36 Explanation:
The correct answer is (C). Any number raised to the power of 1 equals itself, so 31 is equal to 3.
Any number, except zero, that is raised to the 0 power equals 1, so 20 equals 1.
When 1 is raised to any power it always equals 1. The expression becomes:
3 + 1 − 1 = 3
Any number, except zero, that is raised to the 0 power equals 1, so 20 equals 1.
When 1 is raised to any power it always equals 1. The expression becomes:
3 + 1 − 1 = 3
Question 37 |
Carlos is planning to serve lemonade in cone-shaped paper cups at his church picnic. There will be 25 people at the picnic, but he's not sure how much lemonade he will need. As his first step to figure out how much lemonade to prepare, he decides to find the volume of liquid that one of the cone-shaped cups will hold.
He measures one of the cups and finds that it has a diameter of 2.5 inches and a height of 3.625 inches. What is the volume of this cup rounded to the nearest hundredth? (use 3.14 for pi)5.08 in3 | |
5.93 in3 | |
18.61 in3 | |
23.71 in3 |
Question 37 Explanation:
The correct answer is (B). Use the volume formula of a cone given on the Mathematics Reference Sheet:
$V = \dfrac{1}{3} \pi \, r^2 h$
We are given the height and the diameter. The diameter will need to be divided by 2 to get the radius:
$V = \dfrac{1}{3} (3.14) \left(\dfrac{2.5}{2}\right)^2 (3.625)$
Use your calculator to solve:
$V = \dfrac {(3.14) (1.5625) (3.625)}{3}$
$V = 5.93$
$V = \dfrac{1}{3} \pi \, r^2 h$
We are given the height and the diameter. The diameter will need to be divided by 2 to get the radius:
$V = \dfrac{1}{3} (3.14) \left(\dfrac{2.5}{2}\right)^2 (3.625)$
Use your calculator to solve:
$V = \dfrac {(3.14) (1.5625) (3.625)}{3}$
$V = 5.93$
Question 38 |
If the two triangles shown below are similar, what is the value of x?
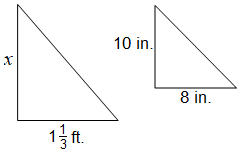
5 inches | |
12.8 inches | |
18 inches | |
20 inches |
Question 38 Explanation:
The correct answer is (D). Problems involving similar figures can be solved using proportions. The issue here is that the two triangles do not agree in measurement. First we must convert the feet measurement into inches. Recall that 12 inches is 1 foot:
$1\dfrac{1}{3} \text{ ft} \ast \dfrac{12 \text{ in}}{\text{ ft}} = 16 \text{ in}$
We can now set up our proportion. Cross multiply to solve for $x$:
$\dfrac{10}{8} = \dfrac{x}{16}$
$8x = 160$
$x = 20$
$1\dfrac{1}{3} \text{ ft} \ast \dfrac{12 \text{ in}}{\text{ ft}} = 16 \text{ in}$
We can now set up our proportion. Cross multiply to solve for $x$:
$\dfrac{10}{8} = \dfrac{x}{16}$
$8x = 160$
$x = 20$
Question 39 |
Li wants to buy as many bags of mulch as possible with his \$305, and he would like them to be delivered to his house. The cost is \$7.50 per bag and there is a \$35.75 delivery charge. The mulch is only sold in full bags. How many bags can Li buy?
35 | |
36 | |
45 | |
46 |
Question 39 Explanation:
The correct answer is (A). From Li’s initial amount of \$305, a flat \$35.75 delivery charge is deducted:
\$305 − \$35.75 = \$269.25.
We can then divide this amount by the cost per bag to find the total number of bags that Li can buy:
\$269.25 ÷ \$7.50 = 35.9 bags. However, the question states that the mulch can only be sold in full bags, so we must round our answer down to ensure that Li does not exceed his budget.
\$305 − \$35.75 = \$269.25.
We can then divide this amount by the cost per bag to find the total number of bags that Li can buy:
\$269.25 ÷ \$7.50 = 35.9 bags. However, the question states that the mulch can only be sold in full bags, so we must round our answer down to ensure that Li does not exceed his budget.
Question 40 |
What is the equation of a line that passes through points $A$ $(1, 2)$ and $B$ $(4, 3)$?
$y = x + 5$ | |
$y = \frac{1}{3}x + 5$ | |
$y = \frac{1}{3}x + \frac{5}{3}$ | |
$y = x + \frac{5}{3}$ |
Question 40 Explanation:
The correct answer is (C). This problem can be solved using two of the formulas: slope of a line and point-slope form of the equation of a line. Use the two given points to first calculate the slope, then substitute one of the given points and the slope into the point-slope form of a line and simplify. Begin by finding the slope:
$m = \dfrac{3 − 2}{4 − 1} = \dfrac{1}{3}$
Using point $A$ $(1, 2)$, write the equation of the line as follows, where $(x_1, y_1)$ are the coordinates of a known point:
$y − y_1 = m(x − x_1)$
$y − 2 = \frac{1}{3}(x − 1)$
$y − 2 = \frac{1}{3}x − \frac{1}{3}$
$y = \frac{1}{3}x − \frac{1}{3} + 2$
$y = \frac{1}{3}x − \frac{1}{3} + \frac{6}{3}$
$y = \frac{1}{3}x + \frac{5}{3}$
$m = \dfrac{3 − 2}{4 − 1} = \dfrac{1}{3}$
Using point $A$ $(1, 2)$, write the equation of the line as follows, where $(x_1, y_1)$ are the coordinates of a known point:
$y − y_1 = m(x − x_1)$
$y − 2 = \frac{1}{3}(x − 1)$
$y − 2 = \frac{1}{3}x − \frac{1}{3}$
$y = \frac{1}{3}x − \frac{1}{3} + 2$
$y = \frac{1}{3}x − \frac{1}{3} + \frac{6}{3}$
$y = \frac{1}{3}x + \frac{5}{3}$
Once you are finished, click the button below. Any items you have not completed will be marked incorrect.
There are 40 questions to complete.
|
List |
